【基础算法】2.高精度&前缀和与差分

系列文章

【基础算法】1.排序及二分

【基础算法】2.高精度&前缀和与差分

【基础算法】3.双指针、位运算、离散化、区间合并

【数据结构】1.链表

【基础算法】习题课1

系列代码

GALA-Lin/Algorithm: CSDN基础算法系列配套代码

一、高精度

小端存储：对大数，如123456879，采用a[0]=9;a[1]=8......;a[8]=1的存储方式，便于进位

1.1 A + B

1. 输入处理：程序首先从标准输入读取两个字符串s1和s2，这两个字符串表示两个非负整数。

2. 字符串转整数向量：将输入的字符串转换为整数向量。转换时，从字符串的末尾开始，逐个字符转为对应的整数值，并存储到向量a和b中。这样做是为了方便从最低有效位（个位）开始进行加法运算。

3. 加法运算：定义了一个add函数来执行两个整数向量的加法。

   • 对齐长度：首先检查两个向量的长度，如果a的长度小于b的长度，则交换它们的位置。这样可以确保在进行加法时，a始终是最长的向量。
   • 逐位相加：使用一个carry变量来记录进位。从最低有效位开始，逐位相加两个向量的对应元素，如果当前位的b向量中没有元素（即i超出b的长度），则只加a中的元素。
   • 处理进位：每次相加的结果先加到carry上，然后将carry对10取模得到当前位的结果，并将其存入结果向量res中。接着，将carry整除10，得到新的进位值。
   • 最终进位检查：在所有位的加法完成后，如果carry仍然大于0，说明最高位有进位，需要将这个进位值也加入结果向量中。

4. 结果输出：将结果向量c从最高有效位开始逐个元素输出到标准输出，形成最终的大整数相加结果。

模拟竖式加法：

在这里插入图片描述

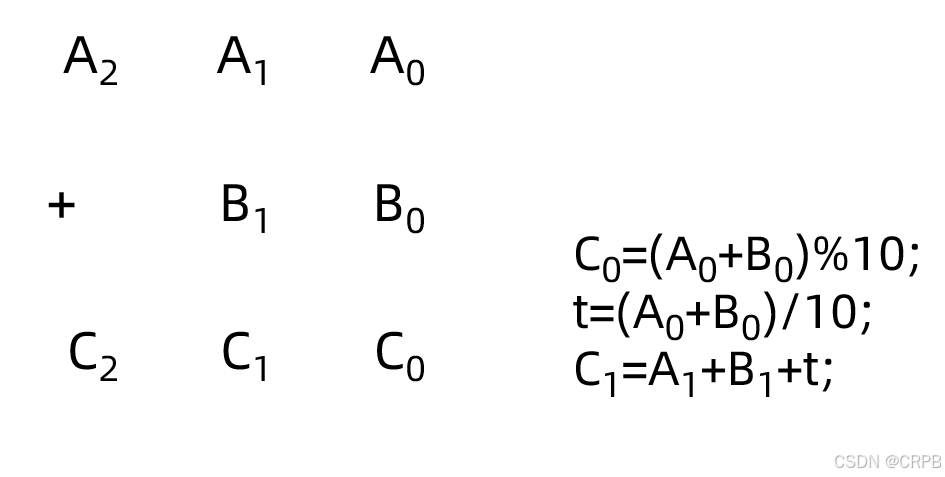
#include <iostream>
#include <vector>
using namespace std;

vector<int> add(vector<int>& a, vector<int>& b){
    vector<int> res(max(a.size(), b.size()));
    int carry = 0;
    for(int i = 0; i < res.size(); i++){
        int sum = (i < a.size()? a[i] : 0) + (i < b.size()? b[i] : 0) + carry;
        res[i] = sum % 10;
        carry = sum / 10;
    }
    if(carry > 0) res.push_back(carry);
    return res;
}

int main() {
    string s1, s2;
    cin >> s1 >> s2;
    vector<int> a(s1.begin(), s1.end());
    vector<int> b(s2.begin(), s2.end());
    //convert char to int
    for(int i = 0; i < a.size(); i++) a[i] -= '0';
    for(int i = 0; i < b.size(); i++) b[i] -= '0';
    vector<int> res = add(a, b);
    for(int i = 0; i < res.size(); i++) cout << res[i];
    cout << endl;
    return 0;
}

1.2 A - B

1. 输入处理：

   • 从标准输入读取两个字符串s1和s2，这两个字符串表示两个整数。
   • 检查每个字符串的第一个字符是否为负号'-'，如果是，则将该字符去掉，并设置相应的标志变量isNegative1和isNegative2为true。

2. 字符串转整数向量：

   • 将去掉负号后的字符串s1和s2的字符逐个转换为整数，并存储到向量a和b中。转换时，从字符串的末尾开始，逐个字符转为对应的整数值，并存储到向量中，以便从最低有效位（个位）开始进行减法运算。

3. 比较函数cmp：

   • 该函数用于比较两个整数向量a和b的大小。
   • 首先比较两个向量的长度，如果长度不同，较长的向量表示较大的数。
   • 如果长度相同，则逐位比较两个向量的元素，从最高有效位开始。第一个不相等的位决定了哪个数更大。

bool cmp(vector<int> &a, vector<int> &b) {
    if(a.size() != b.size()) 
        return a.size() > b.size();
    for(int i =a.size()-1; i>=0; i--) 
        if(a[i] != b[i]) return a[i] > b[i];
    return true;
}

vector<int> sub(vector<int> &a, vector<int> &b) {
    vector<int> res;
    int carry = 0;
    for(int i = 0; i< a.size(); i++) {
        carry = a[i] -carry;
        if(i < b.size()) carry -= b[i];
        res.push_back((carry+10)%10);
        if(carry < 0) carry = 1;
        else carry = 0;
    }
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

4. 减法函数sub：

   • 该函数用于计算两个整数向量的绝对值差。
   • 使用一个carry变量来记录借位信息。从最低有效位开始逐位相减，每次相减的结果先减去carry，如果当前位的b向量中没有元素（即i超出b的长度），则只减a中的元素。
   • 将每次相减的结果加上10后对10取模，得到当前位的结果，并将其存入结果向量res中。如果相减后的结果小于0，说明需要借位，将carry设置为1；否则，将carry设置为0。
   • 在所有位的减法完成后，去除结果向量中末尾的多余零（确保结果没有前导零），然后返回结果向量。

5. 结果处理和输出：

   • 根据输入的两个整数的正负情况，决定如何调用cmp和sub函数，并在输出结果前添加负号'-'（如果结果为负数）。
   • 如果两个数都是负数，则比较它们的绝对值大小。绝对值大的减去绝对值小的，得到的结果可能为正或负，需要根据比较结果决定是否输出负号。
   • 如果第一个数是负数，第二个数是正数，则结果为负，需要输出负号。
   • 如果第一个数是正数，第二个数是负数，则结果为正，直接输出即可。
   • 如果两个数都是正数，则比较它们的大小。较大的数减去较小的数，得到的结果可能为正或负，需要根据比较结果决定是否输出负号。

输入输出控制

    // 处理第一个数是否为负数
    if (s1[0] == '-') {
        isNegative1 = true;
        s1 = s1.substr(1);
    }
    for (int i = s1.size() - 1; i >= 0; i--) a.push_back(s1[i] - '0');

    // 处理第二个数是否为负数
    if (s2[0] == '-') {
        isNegative2 = true;
        s2 = s2.substr(1);
    }
    for (int i = s2.size() - 1; i >= 0; i--) b.push_back(s2[i] - '0');

    if (isNegative1 && isNegative2) { // 两个数都是负数 cmp表示两绝对值大小
        if (cmp(a, b)) {                // 绝对值a>b 即a<b
            vector<int> res = sub(a, b);
            if(res[0]!= 0) printf("-");
            for (int i = res.size() - 1; i >= 0; i--) cout << res[i];
        } else {
            vector<int> res = sub(b, a);
            for (int i = res.size() - 1; i >= 0; i--) cout << res[i];
        }
    } else if (isNegative1) { // 第一个数是负数
        vector<int> res = sub(b, a);
        printf("-");
        for (int i = res.size() - 1; i >= 0; i--) cout << res[i];
    } else if (isNegative2) { // 第二个数是负数
        vector<int> res = sub(a, b);
        for (int i = res.size() - 1; i >= 0; i--) cout << res[i];
    } else { // 两个数都是正数
        if (cmp(a, b)) {
            vector<int> res = sub(a, b);
            for (int i = res.size() - 1; i >= 0; i--) cout << res[i];
        } else {
            vector<int> res = sub(b, a);
            printf("-");
            for (int i = res.size() - 1; i >= 0; i--) cout << res[i];
        }
    }

1.3 A / B

1. 输入处理：

   • 从标准输入读取一个字符串s，表示一个大整数。
   • 从标准输入读取一个整数b，表示除数。

2. 字符串转整数向量：

   • 将字符串s的字符逐个转换为整数，并存储到向量a中。转换时，从字符串的末尾开始，逐个字符转为对应的整数值，并存储到向量中，以便从最低有效位（个位）开始进行除法运算。

3. 除法函数div：

   • 该函数用于计算大整数向量a除以整数b的商，并通过引用参数r返回余数。
   • 初始化一个空的结果向量res和余数r为0。
   • 从向量a的最高有效位开始逐位处理，更新余数r，将当前位的数字加入r，并计算当前位的商。
   • 将当前位的商存入结果向量res中。
   • 更新余数r为当前位相除后的余数。
   • 处理完所有位后，将结果向量res反转，以便从最高有效位开始存储商的每一位。
   • 去除结果向量中末尾的多余零（确保结果没有前导零），然后返回结果向量。

4. 结果输出：

   • 将商的向量逐位输出为字符串形式。
   • 最后输出换行符endl。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 将一个大数（以向量形式存储）除以一个整数b，并返回商的向量形式，同时通过引用参数r返回余数
vector<int> div(vector<int> &a, int b, int &r){
    vector<int> res;
    r = 0;
    for(int i= a.size()-1; i >=0; i--){    // 从最高位开始计算
        r = r*10 + a[i];        // 更新余数，将当前位加入
        res.push_back(r/b);      // 计算商，向量形式存储
        r = r%b;                 // 更新余数
    }
    reverse(res.begin(), res.end());
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

int main(){
    string s;
    cin>>s;
    vector<int> a;
    for(int i=s.size()-1; i>=0; i--) a.push_back(s[i]-'0');
    int b ;
    cin>>b;
    int r;
    vector<int> res = div(a, b, r);
    for(int i=res.size()-1; i>=0; i--) cout<<res[i];
    cout<<endl;
    return 0;
}

1.4 A * B

1. 输入处理：

   • 从标准输入读取一个字符串a，整数b，表示一个大整数。

2. 字符串转整数向量：

   • 将字符串a的字符逐个转换为整数，并存储到向量A中。转换时，从字符串的末尾开始，逐个字符转为对应的整数值，并存储到向量中，以便从最低有效位（个位）开始进行乘法运算。

3. 乘法函数mul：

   • 该函数用于计算大整数向量a乘以整数b的积。
   • 初始化一个空的结果向量res和一个临时变量t为0，t用于存储当前位的乘积和进位。
   • 使用一个循环从最低有效位开始逐位处理，循环条件是i < a.size()或t不为0。这样可以确保最后的进位也被处理。
   • 在每次循环中，如果i小于a的大小，则将a[i]乘以b并加到t上。
   • 将t对10取模得到当前位的结果，并将其存入结果向量res中。
   • 将t整除10，更新t为新的进位值。
   • 处理完所有位后，去除结果向量res中末尾的多余零（确保结果没有前导零），然后返回结果向量。

4. 结果输出：将结果向量res从最高有效位开始逐位输出为字符串形式。

#include<iostream>
#include<vector>
using namespace std;

vector<int> mul(vector<int> &a, int b){
    vector<int> res;
    int t = 0;
    for(int i=0; i<a.size()||t; i++){
        if(i<a.size()) t += a[i]*b;
        res.push_back(t%10);
        t /= 10;
    }
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

int main(){
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for(int i=a.size()-1; i>=0; i--) A.push_back(a[i]-'0');
    vector<int> res = mul(A, b);
    for(int i=res.size()-1; i>=0; i--) cout << res[i];
    return 0;
}

二、前缀和

**前缀和：**对数列前i项求和，即S[i]=a[1]+a[2]+a[3]+......+a[i]，数组从a[1]开始存储以确保有S[0]=0

2.1 一维前缀和

计算方法：S[i]=S[i-1]+a[i]

主要应用：S[i]+S[i-j]=a[j+1]+...+a[i]

#include <iostream>
using namespace std;

const int MAXN = 1e5;
int n, a[MAXN], pre[MAXN];

void pre_sum() {
    pre[0] = a[0];
    for (int i = 1; i <= n; i++) {
        pre[i] = pre[i - 1] + a[i];
    }
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    pre_sum();
    for (int i = 1; i <= n; i++) {
        cout << pre[i] << " ";
    }
    int l,r;
    cin >> l >> r;
    cout << l <<"到"<<r<<"的和为：" << pre[r] - pre[l - 1];
    return 0;
}

2.2 二维前缀和

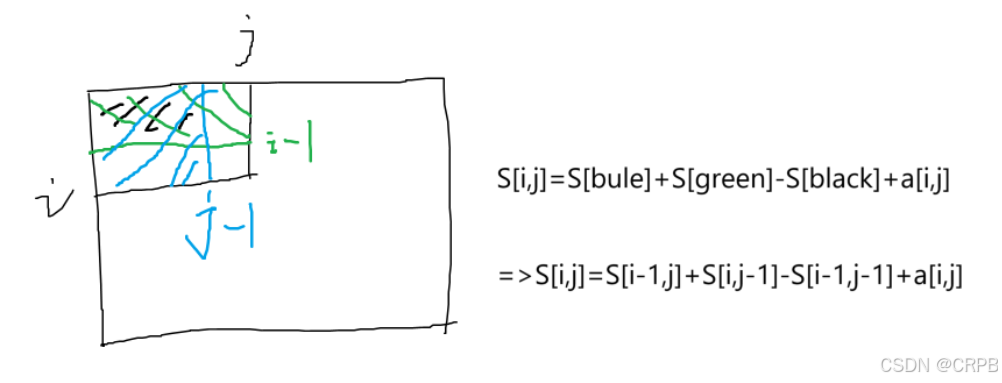
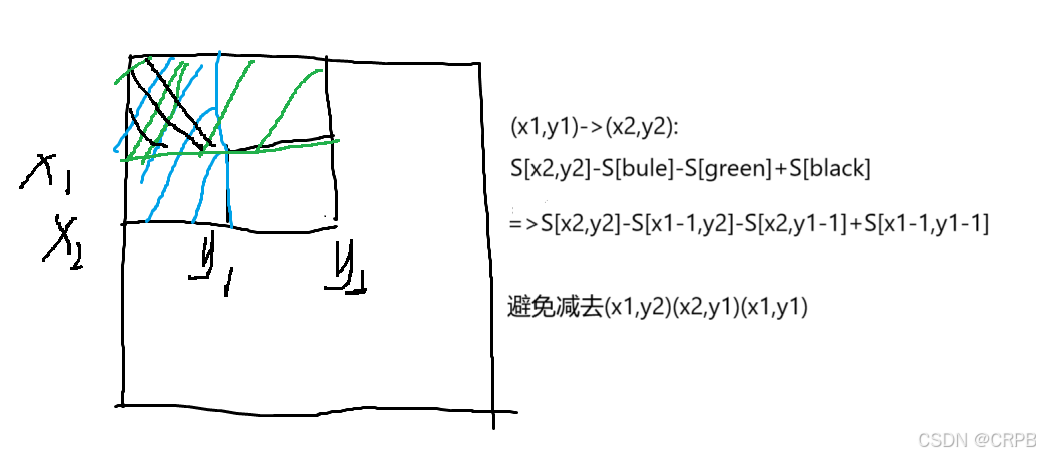
#include <iostream>
using namespace std;

const int MAXN = 1000;
int n, m;
int a[MAXN][MAXN], pre[MAXN][MAXN];

void preSumX2() {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            pre[i][j] = pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1] + a[i][j];
        }
    }
}

int main() {
    cin >> n>>m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
        }
    }
    preSumX2();

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cout << pre[i][j] << " ";
        }
        cout << endl;
    }
    int x1,y1,x2,y2;
    cin >> x1 >> y1 >> x2 >> y2;
    cout <<"("<<x1<<","<<y1<<")"<< " to " << "("<<x2<<","<<y2<<")"<< " sum = " << pre[x2][y2] - pre[x1-1][y2] - pre[x2][y1-1] + pre[x1-1][y1-1];
    return 0;
}

三、差分（前缀和的逆运算）

有数组a[]构造b[]使得a[i]=b[1]+b[2]+...+b[i]

3.1 一维差分

b[1]=a[1];b[2]=a[2]-a[1];b[3]=a[3]-a[2];
...
b[n]=a[n]-a[n-1];

计算方法：

while(i==1){
b[1] +=a[1];	//b[1]=a[1]
b[2] -=a[1];
i++;
}
while(i==2){
b[2] +=a[2];	//b[2]=a[2]-a[1]
b[3] -=a[2];
i++;}
while(i==3){
b[3] +=a[3];	//b[3]=a[3]-a[2]
b[4] -=a[3];
i++;
}
......

所以有

#include <iostream>
using namespace std;
const int MAXN = 1001;
int n;
int arr[MAXN],diff[MAXN];
/*
void difference(int arr[], int n) {
    for (int i = 1; i <= n; i++) {
        diff[i] = arr[i] - arr[i-1];
    }
}
*/
void insert(int l, int c) {
    diff[l]   += c;
    diff[l+1] -= c;
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> arr[i];
    }
/*
    // calculate the difference array
    difference(arr, n);
    for (int i = 1; i <= n; i++) {
        cout << diff[i] << " ";
    }
    cout << endl;
*/
    // insert the original array into the difference array
    for(int i=1;i<=n;i++)
        insert(i,arr[i]);
    cout << "After insert:" << endl;
    for (int i = 1; i <= n; i++) {
        cout << diff[i] << " ";
    }
    return 0;
}

3.2 二维差分(差分矩阵)

a(i,j)表示b(i,j)及其左上方数值之和

计算方法：

void insert(int x1,int x2, int x2,int y2,int c){
    b[x1][y1] += c;
    b[x2+1][y1] -=c;
    b[x1][y2+1] -=c;
    b[x2+1][y2+1] +=c
}