【基础算法】1.排序及二分

[toc]

系列文章

【基础算法】1.排序及二分

【基础算法】2.高精度&前缀和与差分

【基础算法】3.双指针、位运算、离散化、区间合并

【数据结构】1.链表

【基础算法】习题课1

系列代码

GALA-Lin/Algorithm: CSDN基础算法系列配套代码

参考资料

1. Acwing算法基础课
2. Hello Algorithm

一、排序

1.1 快速排序

1.1.1 算法流程

将比基准大的数放在基准右边；比基准小的放在基准左边

1. 选取数组最左端元素作为基准数，初始化两个指针 i 和 j 分别指向数组的两端。
2. 设置一个循环，在每轮中使用 i（j）分别寻找第一个比基准数大（小）的元素，然后交换这两个元素。
3. 循环执行步骤 2 ，直到 i 和 j 相遇时停止，最后将基准数交换至两个子数组的分界线。

例如：

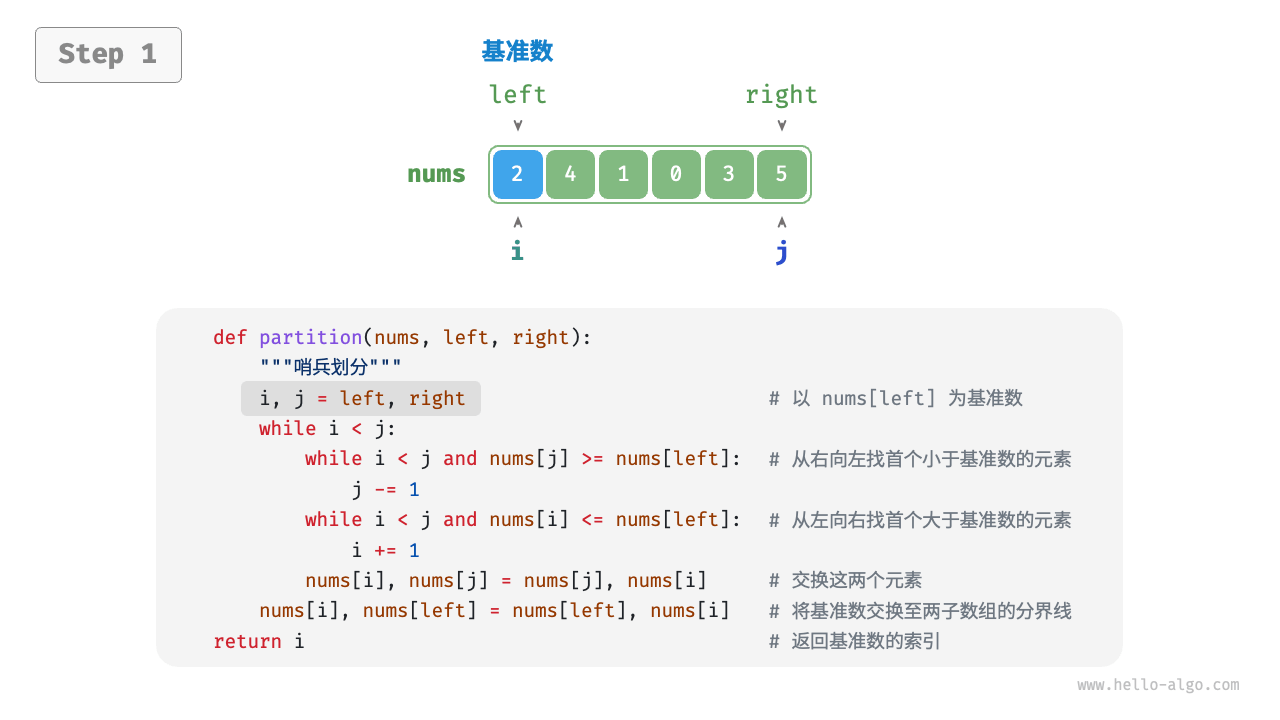
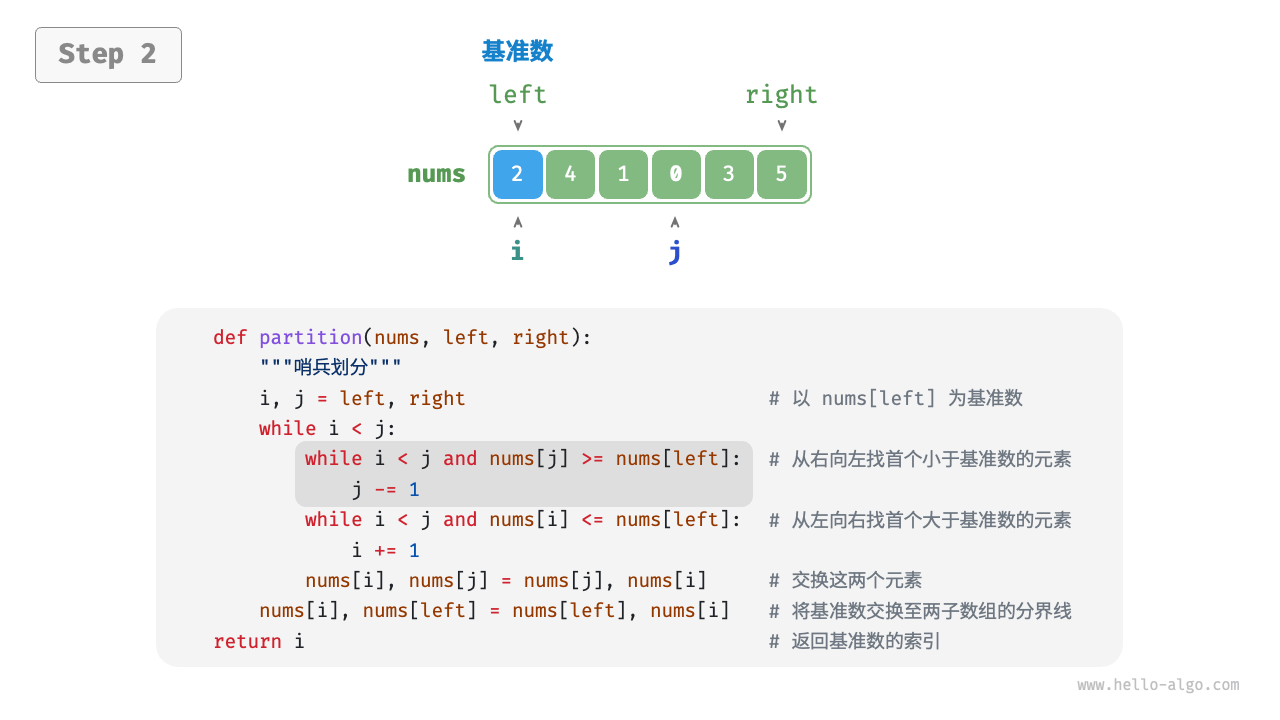
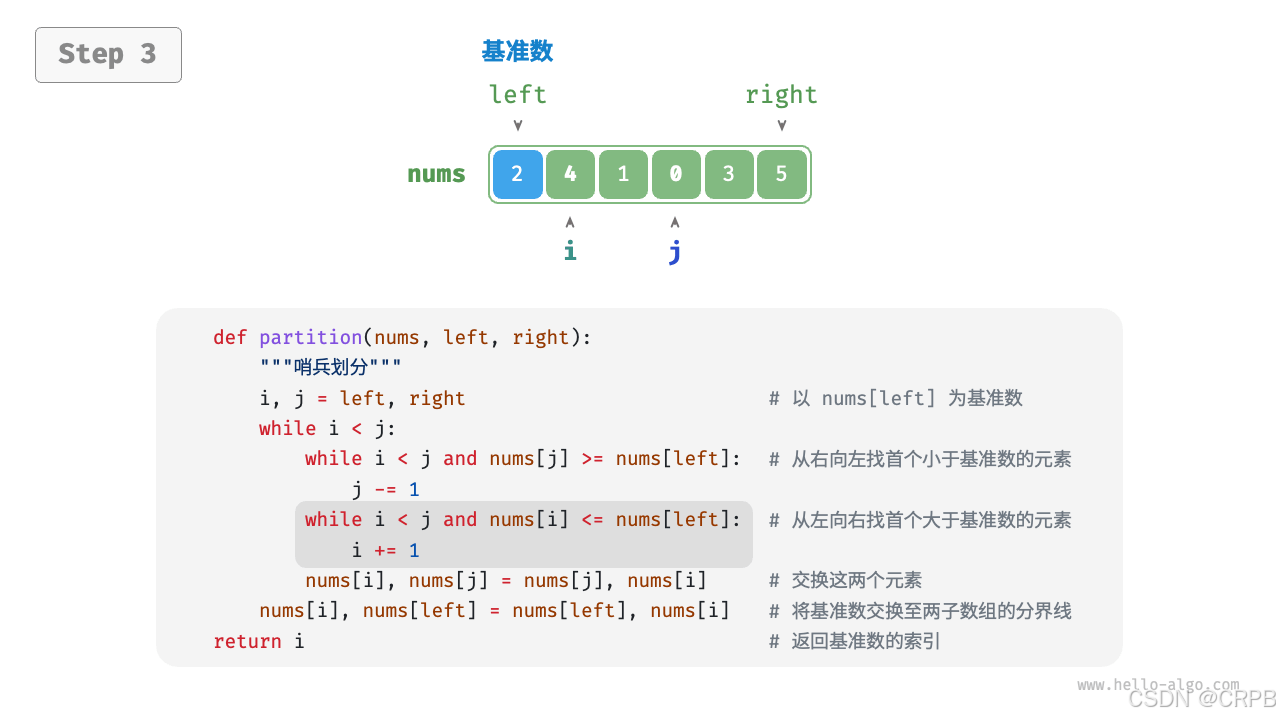
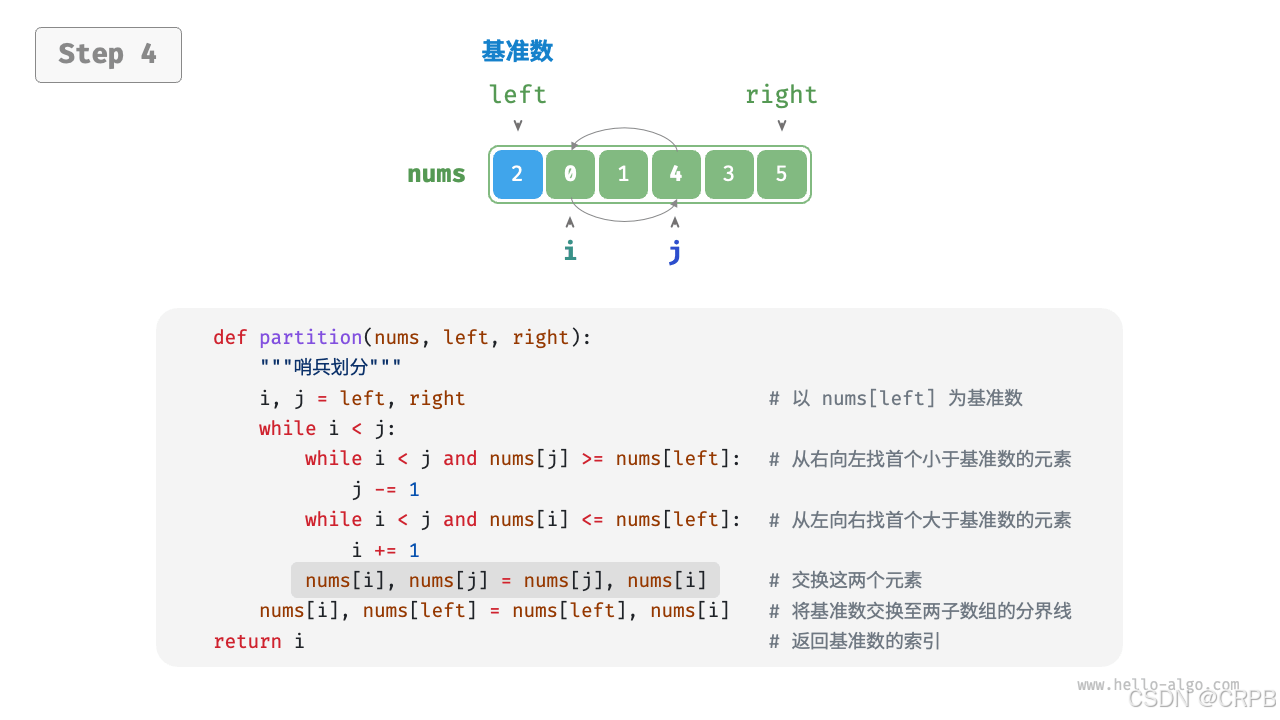
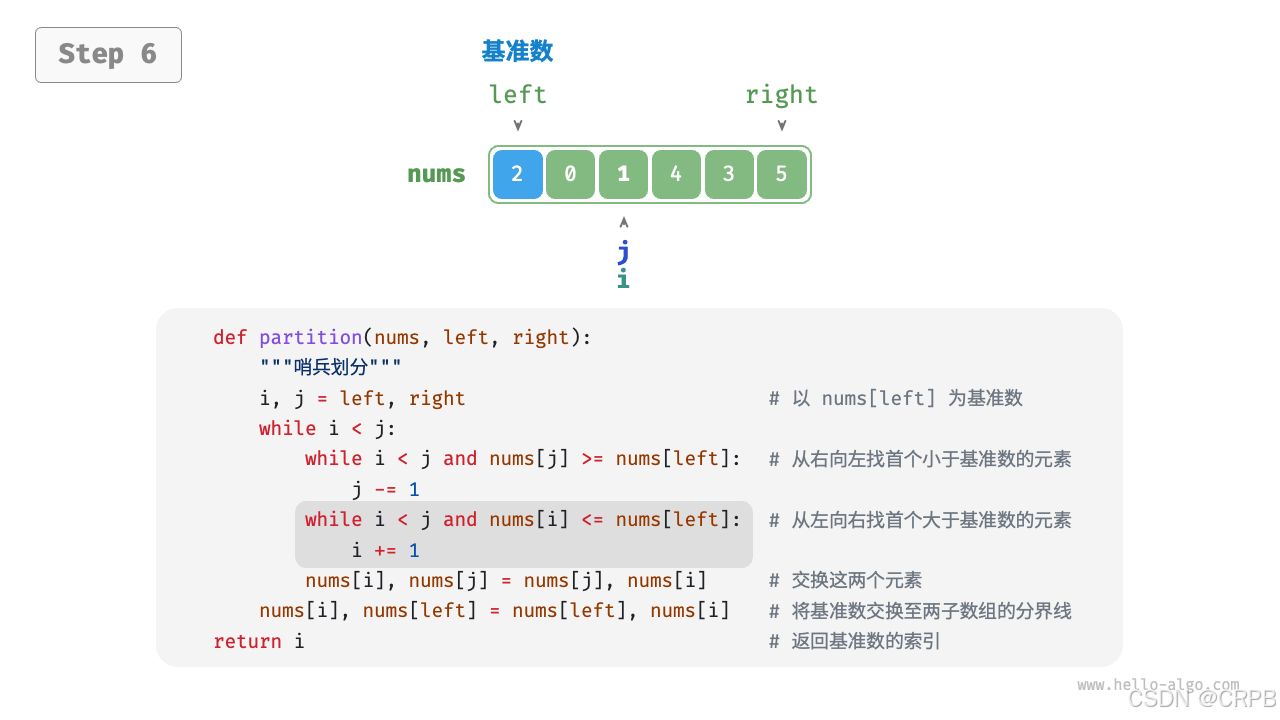
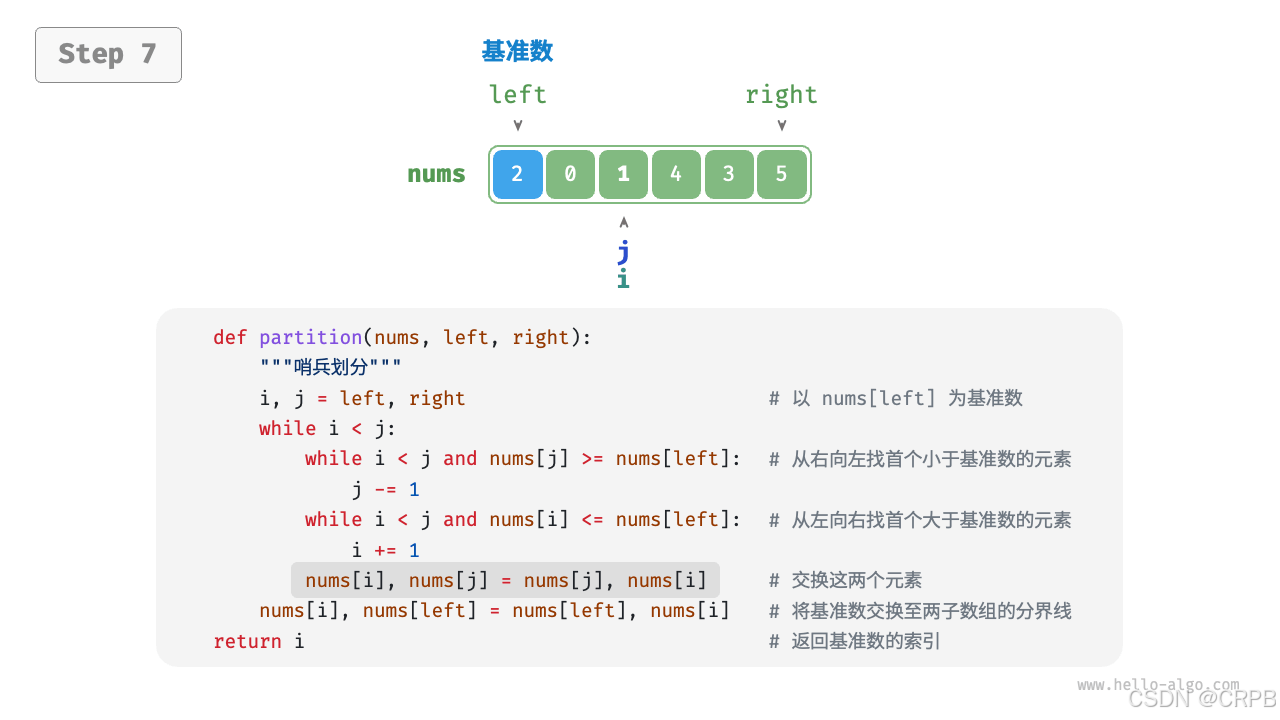
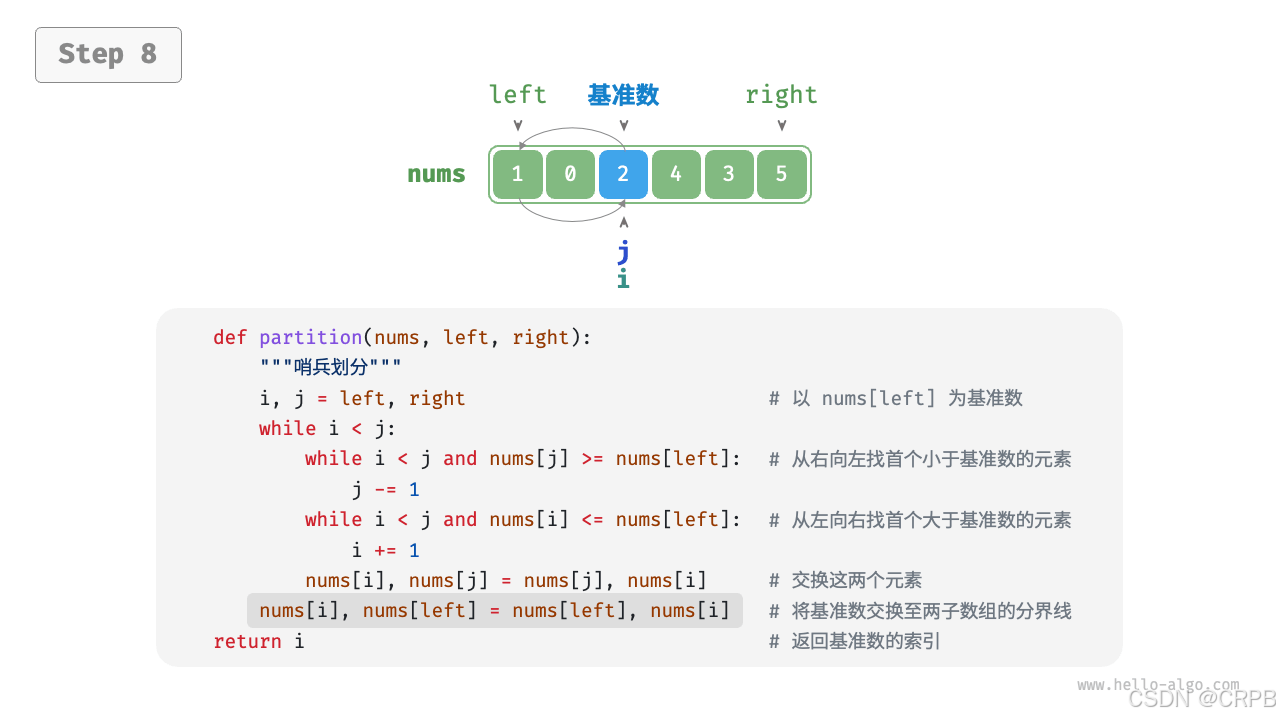
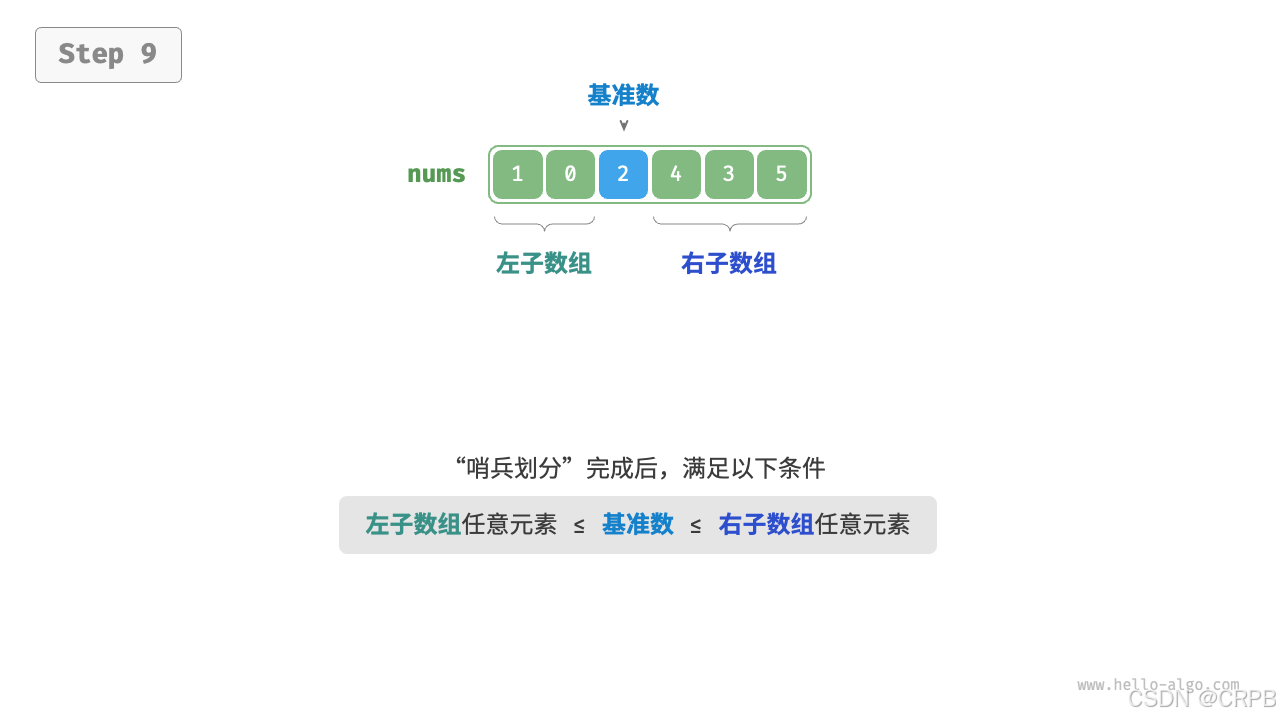
流程如下：

1.1.2 示例代码

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

作者：yxc
链接：https://www.acwing.com/blog/content/277/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1.1.3 例题

1. poj:2388 -- Who's in the Middle
2. 宝藏排序Ⅰ - 蓝桥云课

1.2 归并排序

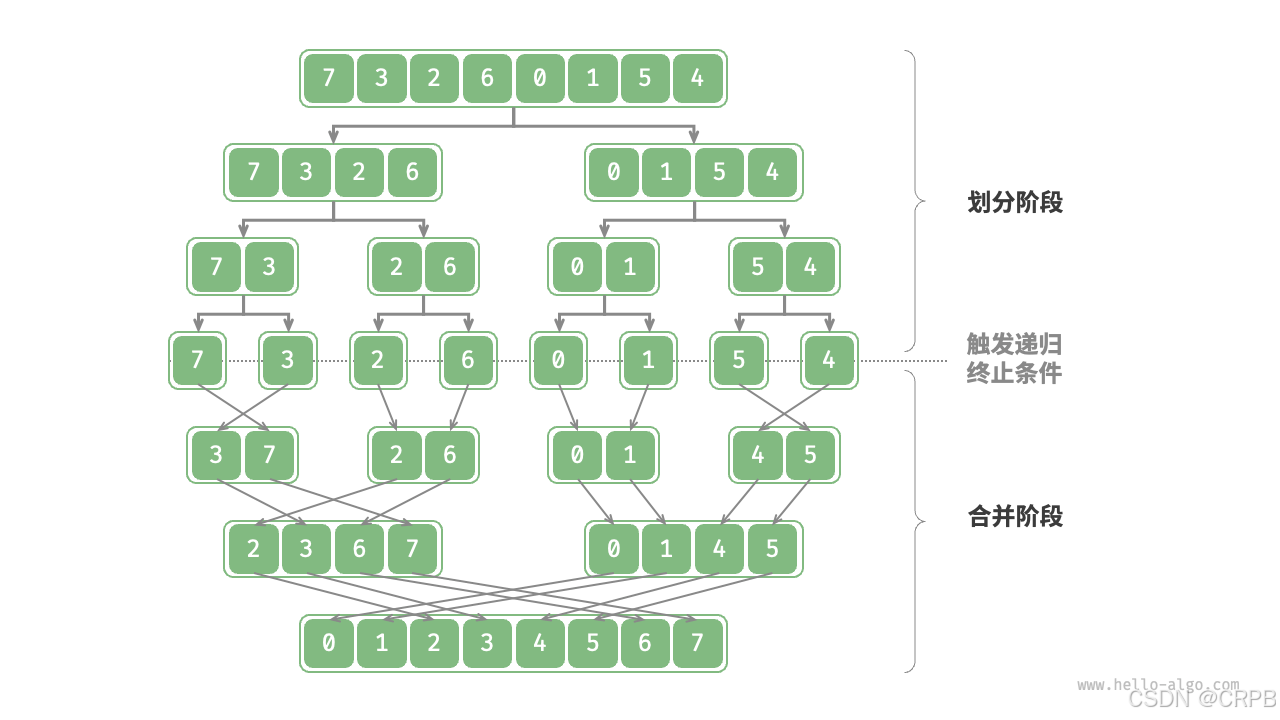
观察发现，归并排序与二叉树后序遍历的递归顺序是一致的。

• 后序遍历：先递归左子树，再递归右子树，最后处理根节点。
• 归并排序：先递归左子数组，再递归右子数组，最后处理合并。

1.2.1 算法流程


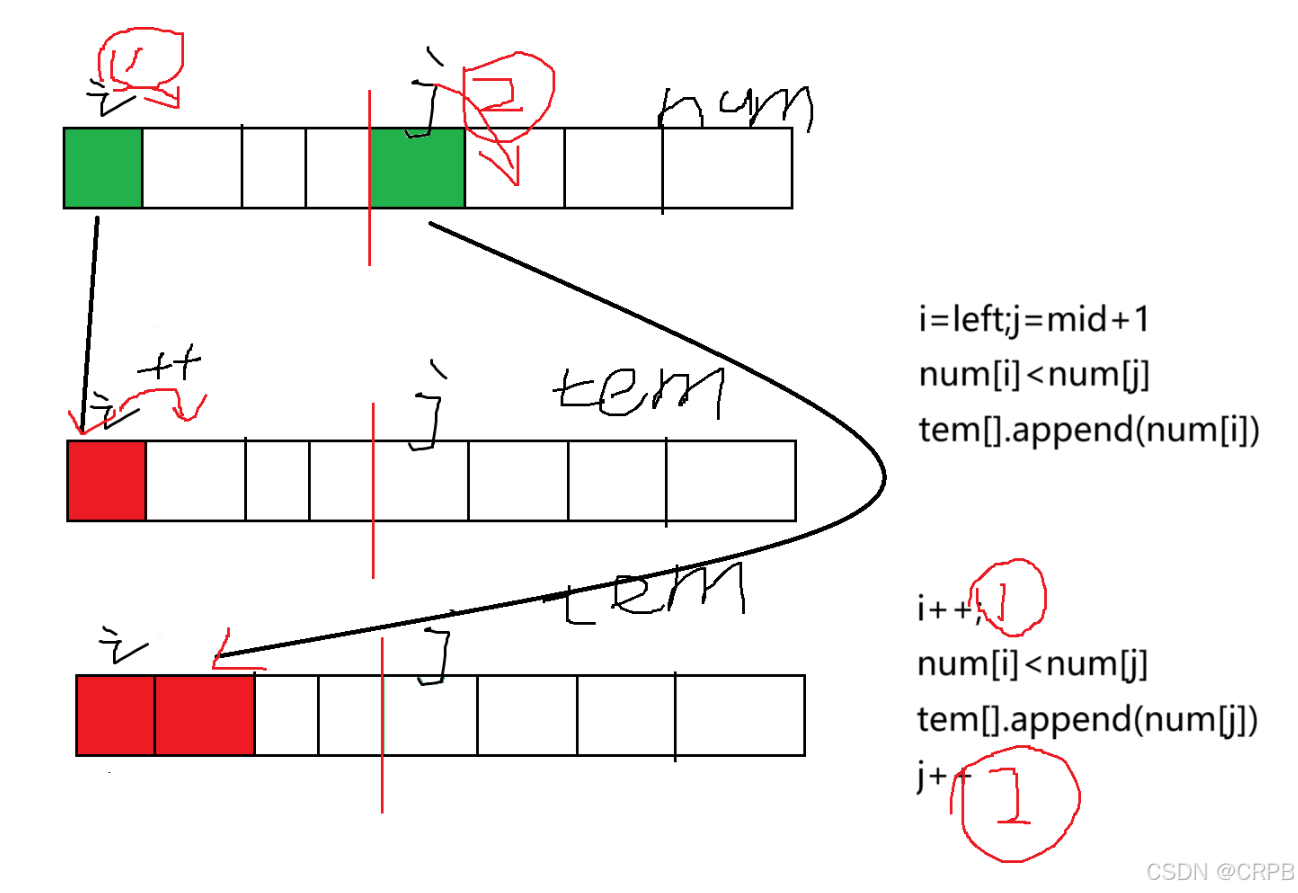
1.2.2 示例代码

/* 合并左子数组和右子数组 */
void merge(int nums[], int left, int mid, int right) {
    // 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]
    // 创建一个临时数组 tmp ，用于存放合并后的结果
    int tmp[right - left + 1];
    // 初始化左子数组和右子数组的起始索引
    int i = left, j = mid + 1, k = 0;
    // 当左右子数组都还有元素时，进行比较并将较小的元素复制到临时数组中
    while (i <= mid && j <= right) {
        if (nums[i] <= nums[j])
            tmp[k++] = nums[i++];
        else
            tmp[k++] = nums[j++];
    }
    // 将左子数组和右子数组的剩余元素复制到临时数组中
    while (i <= mid) {
        tmp[k++] = nums[i++];
    }
    while (j <= right) {
        tmp[k++] = nums[j++];
    }
    // 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
    for (k = 0; k < sizeof(tmp) / sizeof(tmp[0]); k++) {
        nums[left + k] = tmp[k];
    }
}

/* 归并排序 */
void mergeSort(int nums[], int left, int right) {
    // 终止条件
    if (left >= right)
        return; // 当子数组长度为 1 时终止递归
    // 划分阶段
    int mid = left + (right - left) / 2;    // 计算中点
    mergeSort(nums, left, mid);      // 递归左子数组
    mergeSort(nums, mid + 1, right); // 递归右子数组
    // 合并阶段
    merge(nums, left, mid, right);
}

1.2.3 例题

1. 实现归并排序 - 蓝桥云课
2. 65. 数组中的逆序对 - AcWing题库
3. hdu:Problem - 4911

1.3 小结

快速排序与归并排序均采用分治思想
快速排序：

1. 选择基准：从数组中选择一个元素作为基准（pivot）。例如，数组的第一个元素 arr[left]，或者arr[(left+right)/2]。

2. 分区操作：将大于/等于（小于/等于）基准的值放在一边，小于/等于（大于/等于）基准的放在另外一边。在基准两边设置两个指针 i 和 j，i 从左向右扫描找到大于基准的元素，j 从右向左扫描找到小于基准的元素，然后交换这两个元素的位置。这个过程一直重复直到 i 和 j 相遇。

3. 交换基准：当 i 和 j 相遇后，将基准元素与 j 指针所指向的元素交换，这样基准元素就被放置在了正确的位置上。

4. 递归排序：当left大于或等于right时，递归结束，即子数组的长度为0或1，这时数组已经被排序。

归并排序：

1. 分解：将数组分成两个子数组，递归地对每个子数组进行排序。分解的终止条件是子数组的长度为1，因为长度为1的数组必然是有序的。
2. 合并：将两个排序好的子数组合并成一个有序的数组。合并的过程是将两个子数组中的元素按顺序复制到一个临时数组中，然后将临时数组中的元素复制回原数组的对应位置。

二、二分

2.1 整数二分

2.1.1 示例代码

整数二分算法模板 —— 模板题 AcWing 789. 数的范围

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

Note

作者：yxc
链接：https://www.acwing.com/blog/content/277/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

2.1.2 例题

P2249 【深基13.例1】查找 - 洛谷 （哈希）

P1102 A-B 数对 - 洛谷

18.分巧克力 - 蓝桥云课

2.2 浮点数二分

2.2.1 示例代码

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

Note

作者：yxc
链接：https://www.acwing.com/blog/content/277/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

2.2.2 例题

P1024 [NOIP2001] 提高组 一元三次方程求解 - 洛谷
第十二届蓝桥杯B组C/C++省赛—H题（杨辉三角）博客