【基础算法】3.双指针、位运算、离散化、区间合并

@[toc]

系列文章

【基础算法】1.排序及二分

【基础算法】2.高精度&前缀和与差分

【基础算法】3.双指针、位运算、离散化、区间合并

【数据结构】1.链表

【基础算法】习题课1

系列代码

GALA-Lin/Algorithm: CSDN基础算法系列配套代码

一、双指针

例如：

• 归并排序中合并两个有序序列

  while (i <= mid && j <= right) {

     if (nums[i] <= nums[j])

       tmp[k++] = nums[i++];

    else

      tmp[k++] = nums[j++];

  }

• 快速排序

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

示例模板

for(int i=0,j=0;i<n;i++){
    while(j<=i && check(j,i)) j++;
    ......
}

二、位运算

2.1 n>>k&1

**作用：**求n的二进制表示中第k位值

2.2lowbit(x)

**作用：**返回x的有最后一位1
实现方法：x&-x
-x的储存方式为其补码，即取反加1：~x+1
x&-x=x&(~x+1)

如图：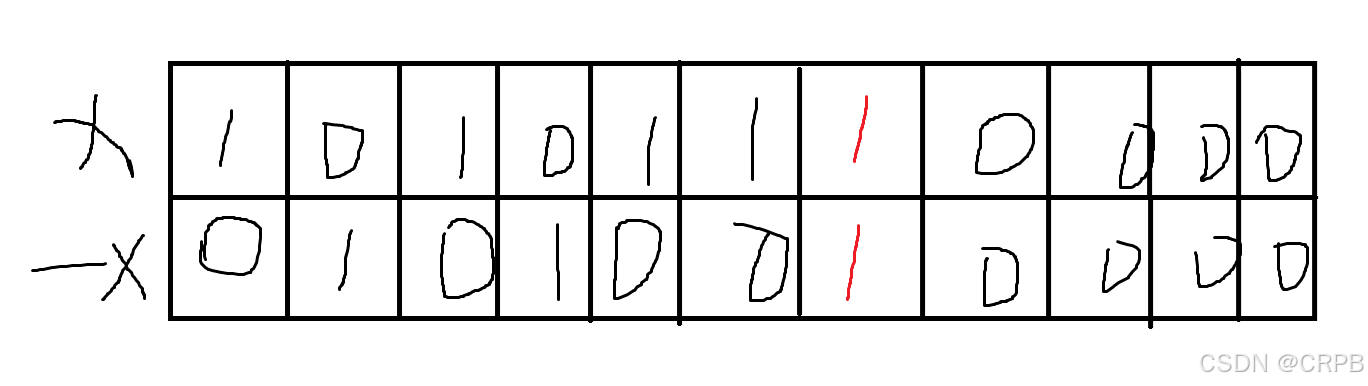

三、离散化

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。

通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。

例如：原数据：1,999,100000,15；处理后：1,3,4,2；

原数据：{100,200}，{20,50000}，{1,400}；处理后：{3,4}，{2,6}，{1,5}；

步骤

1. 排序

2. 去重
   （但是有时候会把相同的元素根据输入顺序离散化为不同的数据。比如将副本按值从小到大排序，当值相同时，按出现顺序从小到大排序。）

3. 查找原数组的每一个元素在副本中的位置，位置即为排名，将其作为离散化后的值

示例代码

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<int> alls;
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}

int main()
{
    vector<int> a;
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        a.push_back(x);
        alls.push_back(x);
    }
    sort(a.begin(), a.end());
    sort(alls.begin(), alls.end());
    for(int i=0;i<alls.size();i++)
        cout<<alls[i]<<" ";
    cout<<endl;
    alls.erase(unique(alls.begin(), alls.end()), alls.end()); //去重
    for (int i = 0; i < n; i++)
    {
        int pos = find(a[i]);
        cout << pos << " ";
    }
    return 0;
}

四、区间合并

给定2个闭区间 [a1,b1],[a2,b2]，判断这两个区间能否合并成为一个新的区间。
任意两个相邻或相交的闭区间可以合并为一个闭区间。例如，[1,2] 和 [2,3] 可以合并为[1,3] ；[1,3] 和 [2,4] 可以合并为 [1,4]，但是 [1,2] 和 [3,4] 不可以合并。
我们的任务是判断这两个区间是否可以最终合并为一个闭区间，如果可以，输出合并的新区间，否则输出-1 。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
int main(void)
{
	vector<pair<long long, long long>> segs;
	for (int i = 0; i < 2; i++)
	{
		long long st, ed;
		scanf("%lld%lld", &st, &ed);
		segs.push_back({ st,ed });
	}
	sort(segs.begin(), segs.end());
	if (segs[0].second < segs[1].first) cout << -1 << endl;
	else
	{
		long long x = segs[1].second > segs[0].second ? segs[1].second : segs[0].second;//把最大的右端点更新一下
		cout << segs[0].first << ' ' << x << endl;
	}
	return 0;
}