【基础算法】2.二分与前缀和习题

[toc]

系列文章

【基础算法】1.排序及二分

【基础算法】2.高精度&前缀和与差分

【基础算法】3.双指针、位运算、离散化、区间合并

【数据结构】1.链表

【基础算法】习题课1

系列代码

GALA-Lin/Algorithm: CSDN基础算法系列配套代码

730. 机器人跳跃问题 - AcWing题库

题目描述

机器人正在玩一个古老的基于 DOS 的游戏。

游戏中有 N+1座建筑——从 0 到 N 编号，从左到右排列。

编号为 0 的建筑高度为 0 个单位，编号为 i 的建筑高度为 H(i) 个单位。

起初，机器人在编号为 0 的建筑处。

每一步，它跳到下一个（右边）建筑。

假设机器人在第 k 个建筑，且它现在的能量值是 EE，下一步它将跳到第 k+1 个建筑。

如果 H(k+1)>E，那么机器人就失去H(k+1)−E 的能量值，否则它将得到 E−H(k+1)的能量值。

游戏目标是到达第 N 个建筑，在这个过程中能量值不能为负数个单位。

现在的问题是机器人至少以多少能量值开始游戏，才可以保证成功完成游戏？

输入格式

第一行输入整数 N。

第二行是 N 个空格分隔的整数，H(1),H(2),…,H(N)H(1),H(2),…,H(N) 代表建筑物的高度。

输出格式

输出一个整数，表示所需的最少单位的初始能量值上取整后的结果。

解题思路

（寻求最小/大普遍二分、贪心、搜索、DP）

1.递推

• H(k+1)>E,E-H(k+1)−E = 2E-H(k+1)
• H(k+1)<=E,E+E-H(k+1) = 2E-H(k+1)

如果设机器人初始能量值 E0 为 x ，则 E1 = 2E0 - H(1) = 2x - H(1) ;

E2 = 4x - 2H1 -H2 ; E3 = 8x - 4H1 -2H2 -H3 ......

让每个 Ei > 0 ,然后得到一系列方程把 x 求解出来

所以有x>=H1/2+H2/4+H3/8+...+Hn/2^n

2.二分

二分条件：

• 二段性：指一个问题可以被划分为连续的两部分，其中一部分满足某个特定条件，而另一部分不满足。这种性质使得二分算法能够通过每次排除一半的搜索空间，快速定位到目标值或分界点。
• **单调性：**如果 x 满足条件，那么所有大于 x 的肯定也满足条件；如果 x不满足条件，那么所有小于 x的肯定也不满足条件

单调性包含于二段性，单调毕可二分，反之不一定。

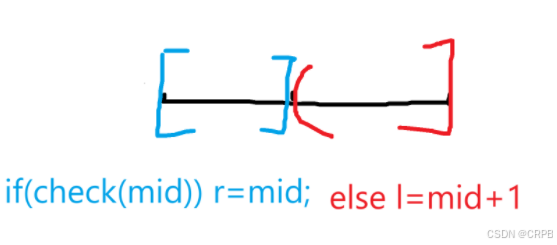
check()：

由单调性可知：

if(check(mid))，那么x肯定mid及其右边部分都可以，为求最小值，使r=mid,查找<=mid的符合条件的值；

else，那么x肯定>mid，使l=mid+1，查找>mid的符合条件的值。

在这里插入图片描述

3.逆推

CODE

1.递推

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n;
int h[N];
double p[N];//存放2的次幂

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> h[i];

    p[0] = 1;//2^0=1

    double res = 0;
    for(int i = 1; i <= n; i++)
    {
        p[i] = p[i - 1] * 2;
        res += 1.0 / p[i] * h[i];
    }

    cout << ceil(res) << endl;

    return 0;
}

作者：Snowing
链接：https://www.acwing.com/solution/content/90581/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

2.二分

3.逆推

99. 激光炸弹 - AcWing题库

题目描述

地图上有N个目标点，用整数Xi,Yi表示目标在地图上的位置，每个目标都有一个价值Wi。
注意：不同目标可能在同一位置。
现在有一种新型的激光炸弹，可以摧毁一个包含R×R个位置的正方形内的所有目标。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个正方形的边必须和x,y轴平行。

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式

第一行输入正整数N和R，分别代表地图上的目标数目和正方形包含的横纵位置数量，数据用空格隔开。

接下来N行，每行输入一组数据，每组数据包括三个整数Xi,Yi,Wi，分别代表目标的x 坐标，y坐标和价值，数据用空格隔开。

输出格式

输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

数据范围

0≤R≤10^9
0<N≤10000
0≤Xi,Yi≤5000
0≤Wi≤1000

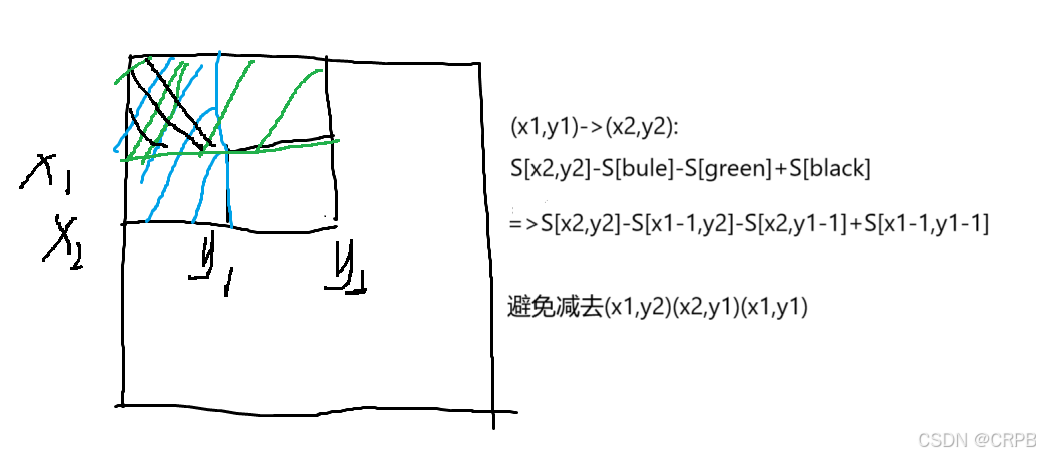
解题思路

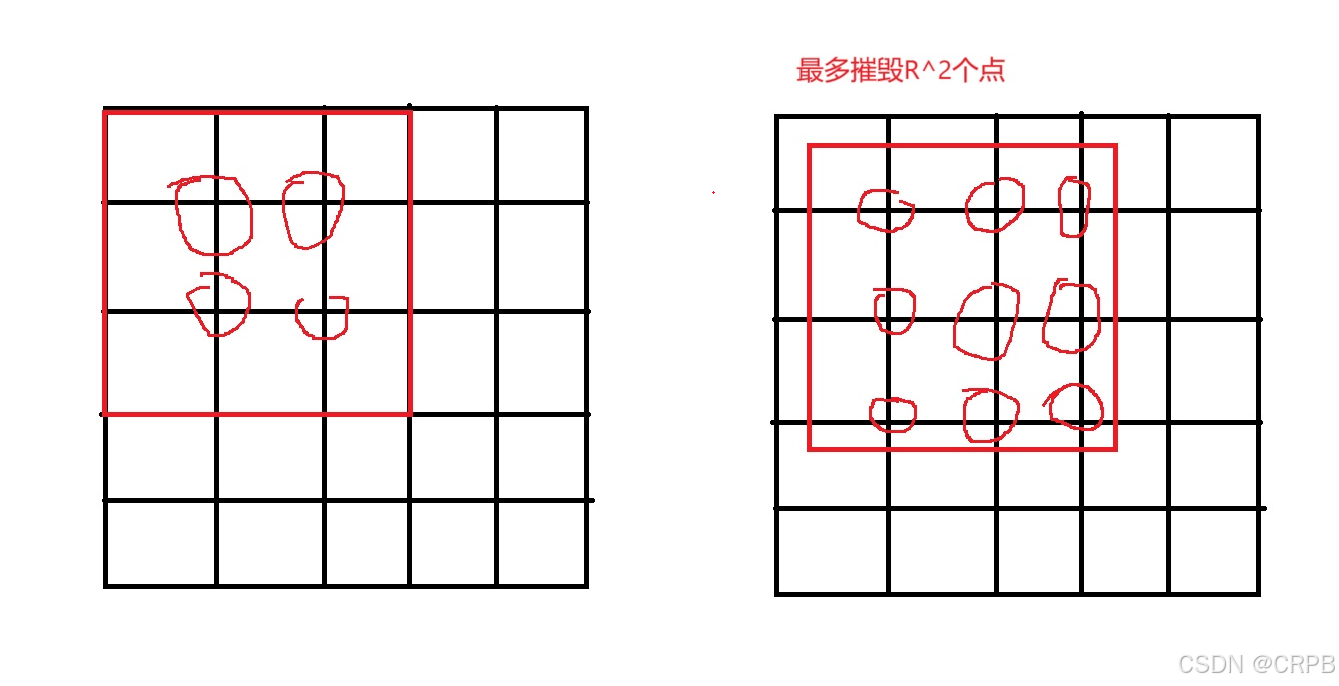
作者：CRPB
原文链接：https://blog.csdn.net/2302_79000266/article/details/144608856
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

📧:Click here to email to

CODE

#include <algorithm>
#include <iostream>

using namespace std;

const int N = 5e3 + 10; //不能开 1e5+10, 内存限制比较严格

int s[N][N];
int n, r;

int main() {
    cin >> n >> r;
    r = min(5001, r); // 因为r最大可以取 10^9
    for (int i = 0; i < n; i++) {
        int x, y, w;
        cin >> x >> y >> w;
        s[++x][++y] += w; //右移一位, 就不需要考虑边界了, 并且必须是+=, 不能是=, 因为1个位置可能有多个目标
    }
    for (int i = 1; i <= 5001; i++) {
        for (int j = 1; j <= 5001; j++) {
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    }
    int ans = 0;
    for (int i = r; i <= 5001; i++) {
        for (int j = r; j <= 5001; j++) {
            ans = max(ans, s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r]);
        }
    }
    cout << ans << endl;
    return 0;
}