Homework5

图像灰度压缩

⼀幅4*4的图像, 灰度值序列如下.请根据课堂上所讲代码,写出构造解的S数组、l数组和b数组, 追踪解的S数组. 需要体现做题过程,如:每⼀轮i的循环写出内部j循环的前两次和最后两次, 内部循环少于等于四次的需要全部j的计算过程

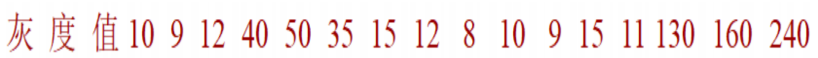
构造阶段的b数组

已知灰度值序列为 10 9 12 40 50 35 15 12 8 10 9 15 11 130 160 240 ，共 n = 16 个元素。
根据 length 函数：

• b[1] = length(10)：

  • i = 10 / 2 = 5 ， k = 2 ；
  • i = 5 / 2 = 2 ， k = 3 ；
  • i = 2 / 2 = 1 ， k = 4 ；
  • i = 1 / 2 = 0 ，返回 k = 4 。

• b[2] = length(9)：

  • i = 9 / 2 = 4 ， k = 2 ；
  • i = 4 / 2 = 2 ， k = 3 ；
  • i = 2 / 2 = 1 ， k = 4 ；
  • i = 1 / 2 = 0 ，返回 k = 4 。

• b[3] = length(12)：

  • i = 12 / 2 = 6 ， k = 2 ；
  • i = 6 / 2 = 3 ， k = 3 ；
  • i = 3 / 2 = 1 ， k = 4 ；
  • i = 1 / 2 = 0 ，返回 k = 4 。

• b[4] = length(40):

  • i = 40 / 2 = 20 ， k = 2 ；
  • i = 20 / 2 = 10 ， k = 3 ；
  • i = 10 / 2 = 5 ， k = 4 ；
  • i = 5 / 2 = 2 ， k = 5 ；
  • i = 2 / 2 = 1 ， k = 6 ；
  • i = 1 / 2 = 0 ，返回 k = 6 。

• b[5] = length(50):

  • i = 50 / 2 = 25 ， k = 2 ；

  • i = 25 / 2 = 12 ， k = 3 ；

  • i = 12 / 2 = 6 ， k = 4 ；

  • i = 6 / 2 = 3 ， k = 5 ；

  • i = 3 / 2 = 1 ， k = 6 ；

  • i = 1 / 2 = 0 ，返回 k = 6 。

$$......$$

• b[16] = length(240):

  • i = 240 / 2 = 120 ， k = 2 ；
  • i = 120 / 2 = 60 ， k = 3 ；
  • i = 60 / 2 = 30 ， k = 4 ；
  • i = 30 / 2 = 15 ， k = 5 ；
  • i = 15 / 2 = 7 ， k = 6 ；
  • i = 7 / 2 = 3 ， k = 7;
  • i = 3 / 2 = 1 ， k = 8;
  • i = 1 / 2 = 0 ， 返回k = 8。

以此类推，计算出完整的 b 数组：b = [0, 4, 4, 4, 6, 6, 6, 4, 4, 4, 4, 4, 4, 4, 8, 8, 8]，索引从0开始

构造阶段的 s 数组和 l 数组

最终结果:

s[]=15 19 23 35 41 47 53 59 65 71 77 82 86 105 113 121，索引从1开始

l[]:1 2 3 4 5 6 7 8 9 10 11 6 7 1 2 3 ，索引从1开始

步骤：

初始化：Lmax = 256 ， header = 11 ， s[0] = 0

• i=1时，b[i]=4,bmax=4,s[1]=s[0]+bmax=4;l[1]=1;s[1]+=header=15
  • i=1<j=2不进入内层循环

+++

• i=2时，b[i]=4,bmax=4,s[2]=s[1]+bmax=19;l[2]=1
  • j=2
    • bmax=4 == b[i-j+1]=b[1]=4 不更新bmax,
    • s[2]=19 > s[0] + j * bmax=0+2*4=8,
    • 所以s[2]=s[0] + j * bmax=2*4=8,l[2]=2,
    • s[2]+=header=19

+++

• i=3时，b[i]=4,bmax=4,s[3]=s[2]+bmax=19+4=23;l[3]=1
  • j=2
    • bmax=4 == b[i-j+1]=b[2]=4不更新bmax,
    • s[3]=23 == s[1] + j * bmax=15+2*4=23,不更新s[3]、l[3]
  • j=3
    • bmax=4 == b[i-j+1]=b[1]=4不更新bmax,
    • s[3]=23 > s[0] + j * bmax=0+3*4=12,
    • 所以s[3]=s[0] + j * bmax=3*4=12,l[3]=3
    • s[3]+=header=12+11=23

+++

• i=4时，b[i]=6,bmax=6,s[4]=s[3]+bmax=23+6=29;l[4]=1
  • j=2
    • bmax=6 > b[i-j+1]=b[3]=4不更新bmax,
    • s[4]=29 < s[2] + j * bmax=19+2*6=41,不更新s[4]、l[4]
  • j=3
    • bmax=6 > b[i-j+1]=b[2]=4不更新bmax,
    • s[4]=29 < s[1] + j * bmax=15+3*6=33,
    • 所以s[4]=s[1] + j * bmax=33,l[4]=3
  • j=4
    • bmax=6 > b[i-j+1]=b[1]=4不更新bmax,
    • s[4]=33 > s[0] + j * bmax=0+4*6=24,
    • 所以s[4]=s[0] + j * bmax=24,l[4]=4`
    • s[3]+=header=24+11=35

+++

• i = 5时，b[5] = 6,bmax = 6，s[5] = s[4] + bmax = 35 + 6 = 41，l[5] = 1

  • j = 2

    • b[i - j + 1] = b[4] = 6 → bmax = max(6, 6) = 6
    • s[i - j] + j * bmax = s[3] + 2 * 6 = 23 + 12 = 35
    • 由于 35 < 41 → 更新 s[5] = 35，l[5] = 2

  • j = 3

    • b[i - j + 1] = b[3] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[2] + 3 * 6 = 19 + 18 = 37
    • 由于 37 > 35 → 不更新

  • j = 4

    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 4 * 6 = 15 + 24 = 39
    • 由于 39 > 35 → 不更新

  • j = 5

    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[0] + 5 * 6 = 30
    • 由于 30 < 35 → 更新 s[5] = 30，l[5] = 5
    • ``s[5] = 30 + 11 = 41`
    • l[5] = 5

+++

• i = 6时，b[6] = 6``bmax = 6，s[6] = s[5] + bmax = 41 + 6 = 47，l[6] = 1

  • j = 2
    • b[i - j + 1] = b[5] = 6 → bmax = max(6, 6) = 6
    • s[i - j] + j * bmax = s[4] + 2 * 6 = 35 + 12 = 47
    • 由于 47 == 47 → 不更新
  • j = 3
    • b[i - j + 1] = b[4] = 6 → bmax = max(6, 6) = 6
    • s[i - j] + j * bmax = s[3] + 3 * 6 = 23 + 18 = 41
    • 由于 41 < 47 → 更新 s[6] = 41，l[6] = 3

  $$......$$

  • j = 5
    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 5 * 6 = 15 + 30 = 45
    • 由于 45 > 41 → 不更新
  • j = 6
    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[0] + 6 * 6 = 36
    • 由于 36 < 41 → 更新 s[6] = 36，l[6] = 6
    • s[6] = 36 + 11 = 47
    • l[6] = 6

+++

• i = 7时，b[7] = 4，bmax = 4，s[7] = s[6] + bmax = 47 + 4 = 51，l[7] = 1

  • j = 2
    • b[i - j + 1] = b[6] = 6 → bmax = max(4, 6) = 6
    • s[i - j] + j * bmax = s[5] + 2 * 6 = 41 + 12 = 53
    • 由于 53 > 51 → 不更新
  • j = 3
    • b[i - j + 1] = b[5] = 6 → bmax = max(4, 6) = 6
    • s[i - j] + j * bmax = s[4] + 3 * 6 = 35 + 18 = 53
    • 由于 53 > 51 → 不更新

  $$......$$

  • j = 6
    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 6 * 6 = 15 + 36 = 51
    • 由于 51 > 47 → 不更新
  • j = 7
    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[0] + 7 * 6 = 42
    • 由于 42 < 47 → 更新 s[7] = 42，l[7] = 7
    • s[7] = 42 + 11 = 53
    • l[7] = 7

+++

• i = 8时，b[8] = 4，bmax = 4，s[8] = s[7] + bmax = 53 + 4 = 57，l[8] = 1

  • j = 2
    • b[i - j + 1] = b[7] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[6] + 2 * 4 = 47 + 8 = 55
    • 由于 55 < 57 → 更新 s[8] = 55，l[8] = 2
  • j = 3
    • b[i - j + 1] = b[6] = 6 → bmax = max(4, 6) = 6
    • s[i - j] + j * bmax = s[5] + 3 * 6 = 41 + 18 = 59
    • 由于 59 > 55 → 不更新

  $$......$$

  • j = 7
    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 7 * 6 = 15 + 42 = 57
    • 由于 57 > 53 → 不更新
  • j = 8
    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[0] + 8 * 6 = 48
    • 由于 48 < 53 → 更新 s[8] = 48，l[8] = 8
    • s[8] = 48 + 11 = 59
    • l[8] = 8

+++

• i = 9时b[9] = 4，bmax = 4，s[9] = s[8] + bmax = 59 + 4 = 63，l[9] = 1

  • j = 2
    • b[i - j + 1] = b[8] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[7] + 2 * 4 = 53 + 8 = 61
    • 由于 61 < 63 → 更新 s[9] = 61，l[9] = 2
  • j = 3
    • b[i - j + 1] = b[7] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[6] + 3 * 4 = 47 + 12 = 59
    • 由于 59 < 61 → 更新 s[9] = 59，l[9] = 3

  $$......$$

  • j = 8
    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 8 * 6 = 15 + 48 = 63
    • 由于 63 > 59 → 不更新
  • j = 9
    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[0] + 9 * 6 = 54
    • 由于 54 < 59 → 更新 s[9] = 54，l[9] = 9
    • s[9] = 54 + 11 = 65
    • l[9] = 9

+++

• i = 10时，b[10] = 4，bmax = 4，s[10] = s[9] + bmax = 65 + 4 = 69，l[10] = 1

  • j = 2

    • b[i - j + 1] = b[9] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[8] + 2 * 4 = 59 + 8 = 67
    • 由于 67 < 69 → 更新 s[10] = 67，l[10] = 2

  • j = 3

    • b[i - j + 1] = b[8] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[7] + 3 * 4 = 53 + 12 = 65
    • 由于 65 < 67 → 更新 s[10] = 65，l[10] = 3

  $$......$$

  • j = 9

    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 9 * 6 = 15 + 54 = 69
    • 由于 69 > 63 → 不更新

  • j = 10

    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6

    • s[i - j] + j * bmax = s[0] + 10 * 6 = 60

    • 由于 60 < 63 → 更新 s[10] = 60，`l[10] = 10``

    • s[10] = 60 + 11 = 71

    • l[10] = 10

+++

• i = 11时,b[11] = 4，bmax = 4，s[11] = s[10] + bmax = 71 + 4 = 75，l[11] = 1

  • j = 2
    • b[i - j + 1] = b[10] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[9] + 2 * 4 = 65 + 8 = 73
    • 由于 73 < 75 → 更新 s[11] = 73，l[11] = 2
  • j = 3
    • b[i - j + 1] = b[9] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[8] + 3 * 4 = 59 + 12 = 71
    • 由于 71 < 73 → 更新 s[11] = 71，l[11] = 3

  $$......$$

  • j = 10
    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 10 * 6 = 15 + 60 = 75
    • 由于 75 > 67 → 不更新
  • j = 11
    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[0] + 11 * 6 = 66
    • 由于 66 < 67 → 更新 s[11] = 66，l[11] = 11
    • s[11] = 66 + 11 = 77
    • l[11] = 11

+++

• i = 12时，b[12] = 4，bmax = 4，s[12] = s[11] + bmax = 77 + 4 = 81，l[12] = 1

  • j = 2
    • b[i - j + 1] = b[11] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[10] + 2 * 4 = 71 + 8 = 79
    • 由于 79 < 81 → 更新 s[12] = 79，l[12] = 2
  • j = 3
    • b[i - j + 1] = b[10] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[9] + 3 * 4 = 65 + 12 = 77
    • 由于 77 < 79 → 更新 s[12] = 77，l[12] = 3

  $$......$$

  • j = 11
    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 11 * 6 = 15 + 66 = 81
    • 由于 81 > 71 → 不更新
  • j = 12
    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[0] + 12 * 6 = 72
    • 由于 72 > 71 → 不更新
    • s[12] = 71 + 11 = 82
    • l[12] = 6

+++

• i=13时，b[13] = 4，bmax = 4，s[13] = s[12] + bmax = 82 + 4 = 86,l[13] = 1

  • j = 2

    • b[i - j + 1] = b[12] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[11] + 2 * 4 = 77 + 8 = 85
    • 由于 85 < 86 → 更新 s[13] = 85，l[13] = 2

  • j = 3

    • b[i - j + 1] = b[11] = 4 → bmax = max(4, 4) = 4
    • s[i - j] + j * bmax = s[10] + 3 * 4 = 71 + 12 = 83
    • 由于 83 < 85 → 更新 s[13] = 83，l[13] = 3

  $$......$$

  • j = 12

    • b[i - j + 1] = b[2] = 4 → bmax = max(6, 4) = 6
    • s[i - j] + j * bmax = s[1] + 12 * 6 = 15 + 72 = 87
    • 由于 87 > 75 → 不更新

  • j = 13

    • b[i - j + 1] = b[1] = 4 → bmax = max(6, 4) = 6

    • s[i - j] + j * bmax = s[0] + 13 * 6 = 78

    • 由于 78 > 75 → 不更新

    • s[13] = 75 + 11 = 86

    • l[13] = 7

+++

• i=14时，b[14] = 8，bmax = 8，s[14] = s[13] + bmax = 86 + 8 = 94，l[14] = 1

  • j = 2

    • b[i - j + 1] = b[13] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[12] + 2 * 8 = 82 + 16 = 98
    • 由于 98 > 94 → 不更新

  • j = 3

    • b[i - j + 1] = b[12] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[11] + 3 * 8 = 77 + 24 = 101
    • 由于 101 > 94 → 不更新

  $$......$$

  • j = 13

    • b[i - j + 1] = b[2] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[1] + 13 * 8 = 15 + 104 = 119
    • 由于 119 > 94 → 不更新

  • j = 14

    • b[i - j + 1] = b[1] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[0] + 14 * 8 = 112
    • 由于 112 > 94 → 不更新
    • s[14] = 94 + 11 = 105
    • l[14] = 1

+++

• i = 15时，b[15] = 8，bmax = 8，s[15] = s[14] + bmax = 105 + 8 = 113，l[15] = 1

  • j = 2

    • b[i - j + 1] = b[14] = 8 → bmax = max(8, 8) = 8
    • s[i - j] + j * bmax = s[13] + 2 * 8 = 86 + 16 = 102
    • 由于 102 < 113 → 更新 s[15] = 102，l[15] = 2

  • j = 3

    • b[i - j + 1] = b[13] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[12] + 3 * 8 = 82 + 24 = 106
    • 由于 106 > 102 → 不更新

  $$......$$

  • j = 14

    • b[i - j + 1] = b[2] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[1] + 14 * 8 = 15 + 112 = 127
    • 由于 127 > 102 → 不更新

  • j = 15

    • b[i - j + 1] = b[1] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[0] + 15 * 8 = 120
    • 由于 120 > 102 → 不更新
    • s[15] = 102 + 11 = 113
    • l[15] = 2

+++

• i=16时，b[16] = 8,bmax = 8，s[16] = s[15] + bmax = 113 + 8 = 121，l[16] = 1

  • j = 2

    • b[i - j + 1] = b[15] = 8 → bmax = max(8, 8) = 8
    • s[i - j] + j * bmax = s[14] + 2 * 8 = 105 + 16 = 121
    • 由于 121 == 121 → 不更新

  • j = 3

    • b[i - j + 1] = b[14] = 8 → bmax = max(8, 8) = 8
    • s[i - j] + j * bmax = s[13] + 3 * 8 = 86 + 24 = 110
    • 由于 110 < 121 → 更新 s[16] = 110，l[16] = 3

  • j = 15

    • b[i - j + 1] = b[2] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[1] + 15 * 8 = 15 + 120 = 135
    • 由于 135 > 110 → 不更新

  • j = 16

    • b[i - j + 1] = b[1] = 4 → bmax = max(8, 4) = 8
    • s[i - j] + j * bmax = s[0] + 16 * 8 = 128
    • 由于 128 > 110 → 不更新
    • s[16] = 110 + 11 = 121
    • l[16] = 3

追踪解的s数组

已知结果

• l 数组：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 6, 7, 1, 2, 3]

计算过程

从 n = 16 开始调用 Traceback 函数：

1. 初始调用：Traceback(16, i, s, l)
   • 递归调用：Traceback(16 - l[16], i, s, l) → Traceback(13, i, s, l)
   • 记录：s[i++] = 13
2. 递归调用：Traceback(13, i, s, l)
   • 递归调用：Traceback(13 - l[13], i, s, l) → Traceback(6, i, s, l)
   • 记录：s[i++] = 6
3. 递归调用：Traceback(6, i, s, l)
   • 递归调用：Traceback(6 - l[6], i, s, l) → Traceback(0, i, s, l)
   • 记录：s[i++] = 0
4. 终止条件：n == 0，返回

追踪解的 S 数组

最终 s 数组存储的是每个分段的起始位置（按调用顺序逆序记录）：

s = [0, 6, 13]

结果解释

• s[0] = 0：第一个分段从像素 1 开始（0 是前一个位置）
• s[1] = 6：第二个分段从像素 7 开始（6 是前一个位置）
• s[2] = 13：第三个分段从像素 14 开始（13 是前一个位置）

验证分段方案

• 分段 1：像素 1-6（长度 6，bmax = 6）
• 分段 2：像素 7-13（长度 7，bmax = 4）
• 分段 3：像素 14-16（长度 3，bmax = 8）

Code

#include <iostream>
#include <vector>
using namespace std;

// 计算整数的二进制位数
int length(int i)
{
    int k = 1;
    i /= 2;
    while (i > 0)
    {
        k++;
        i /= 2;
    }
    return k;
}

// 图像压缩函数
void Compress(int n, int p[], int s[], int l[], int b[])
{
    int Lmax = 256, header = 11;
    s[0] = 0;
    for (int i = 1; i <= n; i++)
    {
        b[i] = length(p[i]);
        int bmax = b[i];
        s[i] = s[i - 1] + bmax;
        l[i] = 1;
        for (int j = 2; j <= i && j <= Lmax; j++)
        {
            if (bmax < b[i - j + 1])
                bmax = b[i - j + 1];
            if (s[i] > s[i - j] + j * bmax)
            {
                s[i] = s[i - j] + j * bmax;
                l[i] = j;
            }
        }
        s[i] += header;
    }
}

// 回溯函数，确定最优分段
void Traceback(int n, int &i, int s[], int l[])
{
    if (n == 0)
        return;
    Traceback(n - l[n], i, s, l);
    s[i++] = n - l[n];
}

// 输出压缩结果
void Output(int s[], int l[], int b[], int n)
{
    cout << "图像压缩后的最小空间为: " << s[n] << endl;
    int m = 0;
    Traceback(n, m, s, l);
    s[m] = n;
    cout << "将原灰度序列分成" << m << "段序列段" << endl;
    for (int j = 1; j <= m; j++)
    {
        l[j] = l[s[j]];
        b[j] = b[s[j]];
    }
    for (int j = 1; j <= m; j++)
    {
        cout << "段" << j << ": 长度=" << l[j] << ", 存储位数=" << b[j] << endl;
    }
}

int main()
{
    // 示例灰度值序列 (4x4 图像)
    int p[] = {0, 10, 9, 12, 40, 50, 35, 15, 12, 8, 10, 9, 15, 11, 130, 160, 240};
    int n = 16; // 图像像素数

    // 初始化数组
    int *s = new int[n + 1];
    int *l = new int[n + 1];
    int *b = new int[n + 1];

    // 执行压缩
    Compress(n, p, s, l, b);
    // 输出b,s,l数组
    cout << "b数组:" << endl;
    for (int i = 1; i <= n; i++)
    {
        cout << b[i] << " ";
    }
    cout << endl;

    cout << "s数组:" << endl;
    for (int i = 1; i <= n; i++)
    {
        cout << s[i] << " ";
    }
    cout << endl;
    cout << "l数组:" << endl;
    for (int i = 1; i <= n; i++)
    {
        cout << l[i] << " ";
    }
    cout << endl;

    // 输出结果
    Output(s, l, b, n);

    // 释放内存
    delete[] s;
    delete[] l;
    delete[] b;

    return 0;
}

Out Put

b数组:
4 4 4 6 6 6 4 4 4 4 4 4 4 8 8 8 
s数组:
15 19 23 35 41 47 53 59 65 71 77 82 86 105 113 121 
l数组:
1 2 3 4 5 6 7 8 9 10 11 6 7 1 2 3 
图像压缩后的最小空间为: 121
将原灰度序列分成3段序列段
段1: 长度=6, 存储位数=6
段2: 长度=7, 存储位数=4
段3: 长度=3, 存储位数=8

最终分段

• 段 1：像素 1-6（长度 6，b=6）
• 段 2：像素 7-13（长度 7，b=4）
• 段 3：像素 14-16（长度 3，b=8）

总位数：每段头信息11位

$$(6 \times 6 + 7 \times 4 + 3 \times 8) + 3 \times 11 = 121 \, \text{位}$$

最小生成树

在ABCDE各城市间建立通信网络,分别用Prim算法和Kruskal算法构造最小生成树

一、Prim算法（以顶点A为起点）

1. 初始化：

   • 已选顶点 ( U = {A} )，未选顶点 ( V-U = {B,C,D,E} )。
   • 距离数组：dist[B]=25，dist[C]=5，dist[D]=25，dist[E]=45。

2. 迭代选择最近顶点：

   • 第1次：选C（dist[C]=5），更新 dist[B]=7（C-B）、dist[D]=44（C-D）、dist[E]=34（C-E）。
   • 第2次：选B（dist[B]=7），更新 dist[D]=11（B-D）、dist[E]=12（B-E）。
   • 第3次：选D（dist[D]=11），无需更新E（B-E已更优）。
   • 第4次：选E（dist[E]=12），结束。

3. 生成树边：A-C（5）、C-B（7）、B-D（11）、B-E（12），权和 35。

表格表述

迭代次数	已选顶点集合	A	B	C	D	E	新添加边
1		-	25	5*	25	45	A-C
2		-	7*	-	44	34	C-B
3		-	-	-	11*	12*	B-D
4		-	-	-	-	78	B-E

二、Kruskal算法

1. 排序边（升序）： 5（A-C）、7（C-B）、11（B-D）、12（B-E）、25（A-B）......

2. 并查集合并：

   • 选A-C（5）：合并{A,C}。
   • 选C-B（7）：合并{A,C,B}。
   • 选B-D（11）：合并{A,C,B,D}。
   • 选B-E（12）：合并所有顶点，结束。

3. 生成树边：同Prim算法，权和 35。

三、结果验证

• 两种算法均得到最小生成树，边为 A-C（5）、C-B（7）、B-D（11）、B-E（12），权值和 35，无环且连接所有顶点，符合最小生成树定义。

答案：

• Prim算法：按上述步骤选择边，最终生成树边为A-C、C-B、B-D、B-E，权和35。
• Kruskal算法：排序边后依次选择无环边，最终生成树边同上，权和35。

四、Code

4.1 Prime

#include <bits/stdc++.h>
using namespace std;

const int INF = numeric_limits<int>::max();

// Prim算法构造最小生成树
vector<pair<int, int>> prim(int n, vector<vector<int>>& graph) {
    vector<int> visited(n, 0); // 记录顶点是否已被加入生成树
    vector<int> minDist(n, INF); // 每个顶点到生成树的最短距离
    vector<int> parent(n, -1); // 记录每个顶点的父节点
    minDist[0] = 0; // 从顶点0开始

    // 优先队列，按距离最小的顺序弹出
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
    pq.push({0, 0}); // 起始顶点

    while (!pq.empty()) {
        int u = pq.top().second; // 当前顶点
        pq.pop();

        if (visited[u]) continue; // 如果顶点已被访问，跳过
        visited[u] = 1;

        // 遍历与顶点u相邻的顶点
        for (int v = 0; v < n; ++v) {
            if (graph[u][v] != 0 && !visited[v]) { // 如果顶点v未被访问且有边
                if (graph[u][v] < minDist[v]) {
                    minDist[v] = graph[u][v];
                    parent[v] = u;
                    pq.push({minDist[v], v});
                }
            }
        }
    }

    // 构造生成树的边
    vector<pair<int, int>> mst;
    for (int i = 1; i < n; ++i) {
        mst.push_back({parent[i], i});
    }
    return mst;
}

int main() {
    // 定义图的邻接矩阵
    int n = 5;
    vector<vector<int>> graph(n, vector<int>(n, 0));
    graph[0][1] = 25; graph[1][0] = 25; // A-B: 25
    graph[0][2] = 5; graph[2][0] = 5; // A-C: 5
    graph[0][3] = 25; graph[3][0] = 25; // A-D: 25
    graph[0][4] = 45; graph[4][0] = 45; // A-E: 45
    graph[1][2] = 7; graph[2][1] = 7; // B-C: 7
    graph[1][3] = 11; graph[3][1] = 11; // B-D: 11
    graph[1][4] = 12; graph[4][1] = 12; // B-E: 12
    graph[2][3] = 44; graph[3][2] = 44; // C-D: 44
    graph[2][4] = 34; graph[4][2] = 34; // C-E: 34
    graph[3][4] = 78; graph[4][3] = 78; // D-E: 78

    // 使用Prim算法构造最小生成树
    vector<pair<int, int>> mst = prim(n, graph);

    // 输出最小生成树的边
    cout << "Prim算法构造的最小生成树：" << endl;
    for (const auto& edge : mst) {
        cout << char('A' + edge.first) << "-" << char('A' + edge.second) << endl;
    }

    return 0;
}

输出

Prim算法构造的最小生成树：
C-B
A-C
B-D
B-E

4.2 Kruskal

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 并查集（Union-Find）结构
class UnionFind {
public:
    vector<int> parent;

    UnionFind(int size) {
        parent.resize(size);
        for (int i = 0; i < size; ++i) {
            parent[i] = i;
        }
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    void unionSet(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY;
        }
    }
};

// 每条边的结构
struct Edge {
    int u, v, weight;
    Edge(int u, int v, int weight) : u(u), v(v), weight(weight) {}
};

// Kruskal算法构造最小生成树
vector<pair<int, int>> kruskal(int n, vector<Edge>& edges) {
    sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {
        return a.weight < b.weight;
    });

    UnionFind uf(n);
    vector<pair<int, int>> mst;
    for (const auto& edge : edges) {
        int rootU = uf.find(edge.u);
        int rootV = uf.find(edge.v);
        if (rootU != rootV) {
            uf.unionSet(rootU, rootV);
            mst.emplace_back(edge.u, edge.v);
        }
    }
    return mst;
}

int main() {
    // 定义图的边
    int n = 5;
    vector<Edge> edges = {
        Edge(0, 1, 25), Edge(0, 2, 5),Edge(0, 3, 25), Edge(0, 4, 45),
        Edge(1, 2, 7), Edge(1, 3, 11), Edge(1, 4, 12),
        Edge(2, 3, 44), Edge(2, 4, 34),
        Edge(3, 4, 78)
    };

    // 使用Kruskal算法构造最小生成树
    vector<pair<int, int>> mst = kruskal(n, edges);

    // 输出最小生成树的边
    cout << "Kruskal算法构造的最小生成树：" << endl;
    for (const auto& edge : mst) {
        cout << char('A' + edge.first) << "-" << char('A' + edge.second) << endl;
    }

    return 0;
}

输出

Kruskal算法构造的最小生成树：
A-C
B-C
B-D
B-E

算法输出边均为 A-C（5）、C-B（7）、B-D（11）、B-E（12），权值和 35